모델이 서로 다른 training set $D=\{(x_1, y_1),...,(x_n, y_n)\}$을 선택하여 학습했을 때, mean squared error는 다음과 같이 bias와 variance로 분해될 수 있다.
$$E_{D,\epsilon}[(y-\hat{f}(x;D))^2]=(\text{Bias}_D[\hat{f}(x;D)])^2+\text{Var}_D[\hat{f}(x;D)]+\sigma^2$$
where
$$\text{Bias}_D[\hat{f}(x;D)]=E_D[\hat{f}(x;D)]-f(x)$$
$$\text{Var}_D[\hat{f}(x;D)]=E_D[(E_D[\hat{f}(x;D)]-\hat{f}(x;D))^2]$$
이때 $\sigma$는 irreducible error이다.
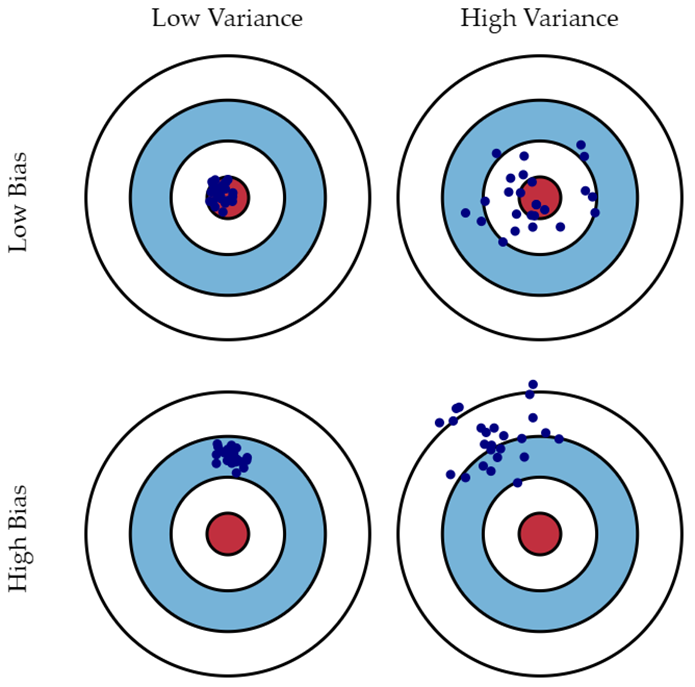
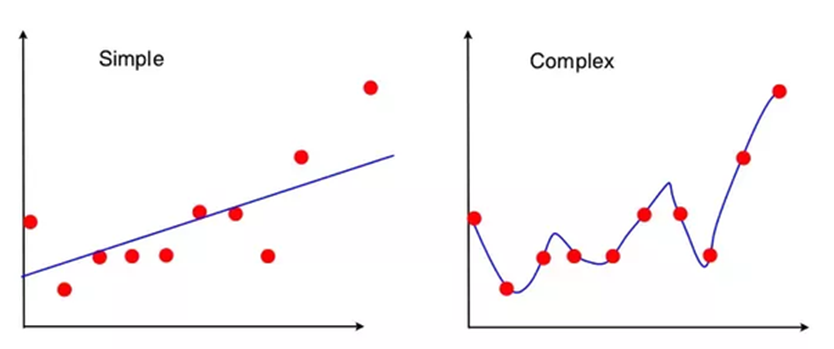
트레이닝 데이터에 없는 x에 대해서 예측할 때, 트레이닝 데이터를 어떻게 추출해서 학습하느냐에 따라 모델의 예측값은 달라지고, 그런 예측값들의 평균과 실제 y값의 차이가 bias, 예측값들이 서로 얼마나 떨어져 있느냐가 variance이다. 언더피팅은 예측값들이 실제 y값과 차이가 클 때, 즉 bias가 큰 상황이고, 오버피팅은 학습한 트레이닝 데이터를 외워 버리기 때문에 트레이닝 데이터에 따라서 모델의 예측값이 오락가락하기 쉬운, 즉 variance가 큰 상황이다.
참고:
머신러닝 - 12. 편향(Bias)과 분산(Variance) Trade-off
편향-분산 트레이드오프 (Bias-Variance Trade-off)는 지도 학습(Supervised learning)에서 error를 처리할 때 중요하게 생각해야 하는 요소입니다. 우선, 아래 그림을 통해 편향(Bias)과 분산(Variance)의 관계를..
bkshin.tistory.com
https://en.wikipedia.org/wiki/Bias%E2%80%93variance_tradeoff
Bias–variance tradeoff - Wikipedia
From Wikipedia, the free encyclopedia Jump to navigation Jump to search Property of a model A function (red) is approximated using radial basis functions (blue). Several trials are shown in each graph. For each trial, a few noisy data points are provided a
en.wikipedia.org
'머신러닝' 카테고리의 다른 글
| Feature Selection (0) | 2022.04.24 |
|---|---|
| Principal Component Analysis (PCA) (0) | 2022.04.24 |
| Regularization (0) | 2022.04.24 |
| Cross Validation (0) | 2022.04.24 |
| Representations of Materials for Machine Learning (0) | 2022.04.24 |


